Physical Review E, 64, 016111, 2001
A model of C60 fullerene, (H2O)60
water and other similar clusters
Sergey Siparov
Department of
Physics, Academy of Civil Aviation, 38 Pilotov St., St.Petersburg, 196210,
Russia
Abstract
The analytical calculation of the partition function
for the lattice gas model of the finite buckminster-ball type cluster and for
the infinite nanotube type cluster is presented. The method of calculation is
based on the Vdovichenko random walk approach. There appeared to be two values
of critical temperature, while the heat capacity in their vicinities is
proportional to 1/(T-Tc).
PACS number(s): 05.50.+q
Introduction
The lattice gas model is well known and is widely used
in statistical mechanics [1]. It has a close relation to the Ising problem of
the phase transition in a ferromagnet [2]. If there is a system of spins
interacting with nearest neighbors and located in the vortices of a lattice of
certain symmetry, then at a certain temperature spontaneous magnetization
appears. Similarly, at a certain temperature a certain atomic structure
consisting of the atoms interacting with nearest neighbors can appear. The
analytical solutions of these problems are known only for the two-dimensional
infinite planar structures such as the square, the triangle and the honeycomb
lattices. In threeа dimensions the
numerical methods are used.
In the field of material science there are two
problems that attract the attention of researchers: the formation, the
structure and the properties of fullerenes and the properties of water in
specific conditions when it demonstrates a kind of a phase transition between
the low-density liquid phase and the high density liquid phase at low
temperatures. Not to discuss these questions in detail, we address the reader
to such reviews as [3], [4] and to the great number of references mentioned
there. The common feature for both of these phenomena could be the symmetry of
the corresponding atomic (molecular) clusters.
The simplest fullerene (not to mention nanotubes so
far) presents a cluster of 60 carbon atoms coordinated as the vortices of a
soccer ball with 12 pentagons and 20 hexagons as facets. Sometimes this
structure is also called the buckminster ball. This conformation is possible
because of the four chemical bonds characterizing a carbon atom. But this is
not the only atom (or molecule) with four bonds. A water molecule, for example,
is able to create a tetrahedrally coordinated open network with the help of
four hydrogen bonds attaching to every oxygen atom. When simulated on a
computer [5] in two dimensions, the ''water molecules'' aggregated in groups that
demonstrated a fivefold orientational order, while hexagonal symmetry was in a
sense also present. This result suggests the idea that if the two-dimensional
surface had a curvature, then the water molecules could form a soccer-ball type
structure having the oxygen atoms in the vortices. The recent results [6] of
the numerical investigation of a microscopical spherical pore containing water
molecules on its inside surface confirms such a possibility, at least in the
case when there is an external field of the pore's walls. But the existence of
C60 аclusters challenges one
to think that (H2O)60 clusters could also form at certain
thermodynamical conditions in the absence of any additional field. In this
case, if these conditions are fulfilled and such clusters start to form, the
density of water will become much less than that of the bulk water, and a low
density liquid phase could appear.
The goal of this paper is to analyze the symmetry
properties of an A60а cluster
and to present the calculation of the partition function for the corresponding
lattice gas model,(here A is an arbitrary atom or molecule initially able to
form a tetrahedral network, and hence, potentially able to form a soccer ball
cluster). We are going to apply the Vdovitchenko method of Ising problem
solution. The detailed description of this method can be found in the classical
course [7]. The method is based on the calculation of the number of random walk
loops on an infinite flat plane with a certain symmetry type of the vortices
distribution. In the problem under discussion here, there is a finite set of
vortices, but it can be shown that the method remains valid for this case too.
Extending the obtained result to an infinite cluster (see below), we will be
able to describe such an interesting physical system as the carbon nanotube. It
will be shown that the method used here is not only applicable to this system,
but being applied to it, the method becomes free from certain approximations
used while dealing with finite A60 clusters.
Calculation of the
partition function
In the further analysis we are going to regard the
random walk on the finite lattice which presents a set of vortices on the
soccer ball cluster surface. Every step of this walk covers a single bond and
leads to one of the neighboring vortices. Every bond of the soccer ball cluster
has one and the same length and every vortex has three nearest neighbors. The
symmetry of the surface is rather complicated due to the existence of both
hexagons and pentagons as its facets.
Thus, first of all, we have to topologically transform
the soccer ball surface lattice in such a way that a convenient procedure for
the random walks calculation could be developed. Let us assume that the bonds
connecting the vortices are elastic and can expand, though every single step in
the future random walk still covers the whole bond between the neighbor
vortices. The topological transformation goes in two stages. On the first stage
we ''pass a cylinder'' through the opposite pentagons of the soccer ball and
let the elastic bonds with vortices stick around the cylinder. On the second
stage we ''inflate'' this cylinder radially and obtain the lattice structure
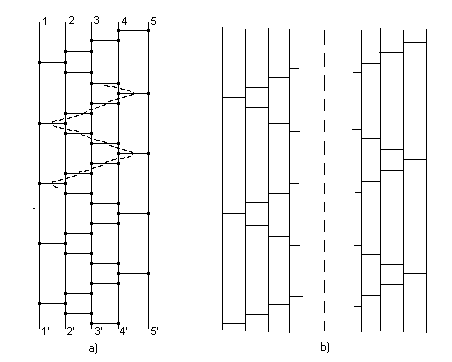
shown on Fig.1a (points i and i') coincide, (i=1...5). Now instead of a ball's surface we obtain a cylinder side
surface and a finite ''square'' lattice with true (physical) periodic conditions. Every vortex has three nearest
neighbors as initially, and every bond will be covered by a single step of a
random walk, according to our assumption. There is an apparent division of
vortices into two sets R and L: R set contains the vortices having right
nearest neighbors, and L set contains
the vortices having left nearest neighbors (part of the border between the sets
is shown on Fig.1a by the dashed line). The obtained structure suggests an idea
to pass to a similar infinite structure following the same rule (Fig.1b). This
new structure is obviously representing a certain nanotube whose wall atoms are
organized in a lattice with the same type of symmetry. One can notice that the
majority of the polygons in such a lattice are hexagons, which is in agreement
with the known structure of carbon nanotubes. In the following calculations we
will discuss simultaneously both the finite and the infinite lattices.
The next step is to find the expression for the
partition function and calculate it. To have a clearer understanding of the
following, it is recommended to refresh in your memory the corresponding
chapter in [7]. Let J be the nearest neighbors interaction energy, then the
expression for the partition function can be written
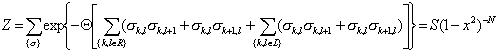ааа ааа(1)
where S{s} means the summation over all possible configurations,
Q
= J/2kT, k is Boltzmann constant, T is the absolute temperature, 1/2 is
due to the double counting of each pair of vortices while summing over both
sets, x = tanh Q,
N is the number of
vortices. Here we preserve for convenience the notation characteristic of a
magnetic system (the obvious correlation between the ''magnetic'' variables
σ(m,l)а = 1, σ(m,2)
= -1 and Уlattice gasФ variables σ(l,1) = 0, σ(l,2)
= 0 is σ(l,1)а =
(1/2)(σ(m,1)а + σ(m,2)
), σ(l,2)а =
(1/2)(σ(m,1)а - σ(m,2)
). The expression for S has the
following form
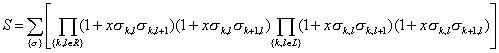ааааа (2)
To calculate the polynomial in equation (2), a diagram
technique developed by Vdovichenko and discussed in [7] can be used. If x corresponds
to a bond between two neighbor vortices, the polynomial will correspond to the
number of loops.
Remark 1. It is important to emphasize that this technique is
designed in such a way that the loops containing the superposed bonds vanish.
That is why this technique remains valid for the case of the finite lattice
discussed here. (This also means that the same technique will apply for various
nanotubes of the same symmetry type.) Notice also, that the summation over k and l here is also different from what it is in the case of an infinite
planar lattice. Equations (1) and (2) give the exact value of the partition
function.
With regard to Remark 1, the result of the calculation
can be written
аааааааааааааааааааааааааааааааааааааааааааа 
аааааааааааааааааааааааааааааааааааааа(3)
ааа where fr аstands for the sum over single loops of r steps each. Now let us introduce Wr(k,l,n ) -- the sum over all possible paths of r steps starting from the given vortex (k0,l0,n0) to the vertex (k,l,n
) in such a way that the
last step to the vertex (k,l,n
) does not take place
from the direction n (n = 1 (right), 2 (up), 3 (left), 4 (down)). According
to the obtained symmetry structure (Fig.1), nа = 3 is
forbidden for (k,l)
in R set, and n а= 1 is
forbidden for (k,l) in L set. Then, similarly to [7], we get
аааааааааааааааааааааааааааааа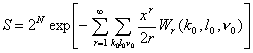 
аааааааааааааааааааааа(4)
It is possible to get the recurrence relations between
Wr+1 and Wr from the definition of Wr(k,l,n
). For R set they can be written as
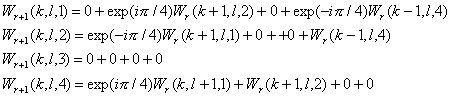ааааааа (5)
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа
Similarly, for L
set, we will get
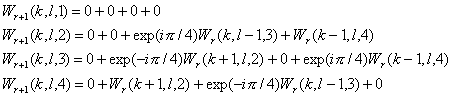ааааааа (6)
The exponential factors correspond to the turns needed
to complete the loops. In a compact form the equations (5-6) can be expressed
as
ааааааааааааааааааааааааааааааааа 
where the matrix L elements can be associated with a ''transition probability''
per step for a randomly walking point. The probability to have a path of r steps will, thus, be given by 
. The diagonal elements of this matrix present the
probability that the randomly walking point will return to its original
position after r steps, and thus,
аааааааааааааааааааааааааааааааааааааааааааааа 
and
аааааааааааааааааааааааааааааааааааааааааааааааааааааа 
аааааааааааааааааааааааааааааааааааааааа(7)
where li are the eigenvalues of the matrix. Substituting
equation (7) into equation (3), we get
ааааааааааааааааааааааааааааааааааааааааааа
аааааааааааааааааааааааааааааааааааааааааааааааааа 
ааааааааааааааааааааааааааааааааааааа(8)
Now we come to the direct calculation of the partition
function and, consequently, we need the form of L matrix.
Remark 2. In our case there are two sets of vortices and,
consequently, there are two systems of equations. This means that the matrix of
coefficients must have a Jordan (normal) form.
To diagonalize matrix L with respect to indices k and l, the Fourier
transformation is most convenient. Though according to the type of structure
presented on Fig.1, k and l vary in different ways, we will
approximate the Fourier transform of L by a common expression
ааааааааааааааааааааааааааааааа 
where 
. Therefore, the matrix of coefficients (i.e. random walk
transition probabilities) will have the form
ааа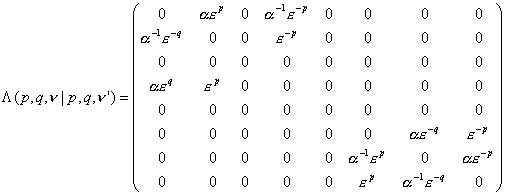 
where a = exp (ip
/4) and e
= 2pi/L. For the given p
and q a simple calculation gives
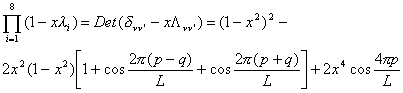аааааааааааааааааааа (9)
Finally, the substitution of equation (9) into equation
(8) and then into equation (1) gives the expression for the partition function Z
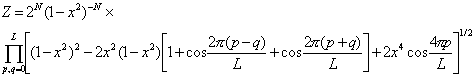аа (10)
This expression is a finite polynomial in case of an A60а model cluster. But for an infinite structure
presented on Fig.2b this polynomial is infinite.
Discussion
In order to describe the critical behavior of the
system and to find the corresponding characteristics, the calculation of the
thermodynamic potential F = - kT ln Z should be performed. It should be mentioned here that
every time we speak of the exact results or of the critical features of the
system's behavior, one should note that in the true sense this can be applied
only to the nanotubes with infinite length, while for the finite-length nanotubes
or for the A60 model clusters the results are approximate.
The logarithm of the product gives the sum. Passing
from the summation to integration is the next approximation: in the case of the
finite A60а model cluster
lattice, the sum is neither infinite nor even very large, though in the case of
an (infinite) nanotube this approximation can lead to an exact result.
Proceeding with the calculation, we obtain
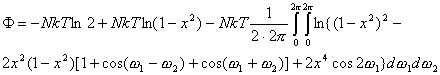аааааааааа (11)
The formation of the soccer ball structure corresponds
to the phase transition, and F function has a singularity at this point. Notice that
when applied to the finite A60 model cluster, the last (approximate)
expression will point not at the true singularity but to a sharp transition. In
our case the singularity corresponds to zero value of the expression under
logarithm. As a function of w1 and
w2 this expression has a minimum when w1
= w2
= 0. This condition
sufficed, the expression under logarithm in equation (11) is equal to 
. The last polynomial is the biquadratic equation with two
positive roots 
. The last fact suggests that there are two critical
temperatures corresponding to the formation of the soccer ball structure. The
analysis of the integral in equation (11) shows that in the vicinity of (xc)2 = 0.39 the
integral is always positive, while in the vicinity of (xc)1 = 0.86 it can take both signs. The
corresponding values of xc аfor the square, the triangle and the
honeycomb infinite lattices are [1] 0.44, 0.27, 0.66. It is interesting to
notice that the direct numerical calculation [8] of xc for the soccer ball structure provides (xc)num = 0.628,
which is equal to (1/2)[(xc)1 + (xc)2]
of the analytical result obtained here.
Remark 3. Here we would like to underline that the well known
result [2] suggests, that a phase transition can only occur in an infinite
system (the thermodynamic limit). Thus, at first glance it seems doubtful that
the critical behavior can be obtained on a lattice with only 60 vortices. The important
particular feature of the finite system under discussion is the true (physical)
periodic conditions which appear to lead to a ''critical'' behavior in this
finite system. As we see from all the argumentation and calculations given above,
we get the same result for the infinite cluster,
and this result does not contradict [9]. But the character of the calculation
procedure which leads to the partition function expression is the same. This
means that the possibility of the critical behavior here is due not to the
infinite number of the counted loops, but to the fact that the majority of
these loops cancel out because of the superposition or intersection of the
loops' bonds. Though the further calculations based on the expression for the partition
function are exact only for the infinite system and are approximate for the
finite system, the character of results must remain the same. The rigorous
mathematical treatment of the role of the true periodical conditions in the
description of the critical behavior of a system constitutes a separate and
wider problem.
Now we can get an expansion of the thermodynamic
potential F in the powers of
t, (t = T - Tc ), where Tc
is a critical temperature related toа xc, (xc = tanh J/2kTc).
The regular part of this expansion can be simply replaced by its value for t = 0, while for its singular term we
get
аааааааааааааааааааааааааааааааааааааааааааа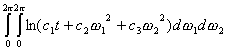 
where c1
, c2, c3 are constants and c1 > 0. Carrying out the integration, we obtain the
singular term of the thermodynamical potential near the transition point in the
form
аааааааааааааааааааааааааааааааааааааааааааааааааа 
ааааааааааааааааааааааааааааааааааааааааааа(12)
The thermodynamical potential appears to be continuous
near the transition point, but the heat capacity C becomes infinite and is proportional to 1/t
аааааааааааааааааааааааааааааааааааааааааааааааааа 
аааааааааааааааааааааааааааааааааааааааааааааа(13)
which differs from the known logarithmic singularity.
In the recent paper [10] there is a plot of the heat capacity vs. temperature
for C60 and C70 fullerenes, and the text near it reads:
''It is interesting to notice that contrary to the majority of organic
substances the fullerenes' heat capacity dependence on temperature has two
inflexion points''. This result based on the analysis of the experimental data
supports the theoretical result obtained here.
In conclusion, we can state the following. In this paper
the theoretical model of an A60 soccer-ball type finite structure
and of a similar symmetry type infinite nanotube structure (Fig.1b) were
discussed in frames of the lattice gas model. To apply the Vdovichenko method
for the partition function calculation, the soccer-ball lattice was
topologically transformed into a lattice on a side surface of a cylinder. Since
the vortices of this lattice fell into two sets, it was essential to present
the matrix of coefficients in a Jordan form. After that, the analytical form of
the partition function for this model was found directly. In the case of the
infinite lattice the expression for the partition function led to the exact
results, while for the finite A60 clusters these results are
approximate. The thermodynamical potential for this model appeared to have two
critical temperatures, corresponding to the lattice formation. This is in
accord with the experimental data for the fullerenes' heat capacity vs.
temperature dependence [10]. The arithmetic mean of the analytically found
critical parameters xc = tanh
J/2kTcн coincides with the value of the same critical parameter
for a soccer ball cluster found numerically [8] with the help of a computer.
The heat capacity singularity appeared to be not logarithmic, but inversely
proportional to the first power of T - Tc.
This model can be used to describe the formation of
such physical systems as carbon fullerenes from the gaseous phase, or the
formation of ''(H2O)60-ice'' clusters from liquid water,
or the formation of the other similar clusters consisting of the other atoms or
molecules able to form a tetrahedrally coordinated network. Besides, this model
is applicable for the description of the formation not only of the classical
buckminster ball fullerene, but for the formation of various nanotubes of the
similar symmetry also. Strictly speaking, a regular nanotube of a certain type
already presents the lattice on a side surface of a
cylinder that was discussed above. In case of long tubes there is no direct
break of the statement made in [9], but as we have shown, the clusters with
true (physical) periodic conditions can demonstrate such a ''critical''
behavior also. The obtained expression for the partition function provides the
possibility to calculate the various thermodynamical parameters of interest.
Acknowledgment
I would like to express my gratitude to Prof.
H.E.Stanley for keeping me informed of the recent developments in water
research and to I.S.Siparov for helpful discussions on geometric transformations.
Bibliography
[1] R.J.Baxter, Exactly Solved Models in Statistical
Mechanics, Academic Press, London, 1982
[2] C.N.Yang. Phys.Rev., 85, (1952), 808
[3] A.V.Eletskii, Uspehi Fizicheskih Nauk, 167 (1997),
945.
[4] H.E.Stanley et al., Physica D 133 (1999), 453.
[5] A.Skibinsky et al. Phys.Rev.E, 60 (1999), 2664.
[6] A.Geiger (private communication)
[7] L.Landau, E.Lifshits. Statistical physics, Nauka,
Moscow, 1984.
[8] S.Buldyrev (private communication)
[9] C.N.Yang and T.D.Lee. Phys.Rev. 87, (1952), 404
[10] V.V.Diky, G.Ya.Kabo. Uspekhi Khimii (Russian
Chemical Review), 69, (2000), 107.
