Бытие и сознание – конструктивный подход*
(послесловие
для заинтересовавшихся)
Напомним, к какому выводу мы
пришли во Введении. Человеческое сознание, обладающее
весьма строгим и a'priori не присущим миру языком логики и математики, не
столько отражает, сколько формирует сначала картину мира на основе
той или иной концепции, а затем, раз уж
мы умудряемся заставить эту картину "работать" на себя, и сам мир.
Сопоставим это с выводами последней главы о том, что в зависимости от того, какие естественнонаучные
концепции будут полагаться в основу наших знаний о природе, а, значит, и в
основу дальнейшей как познавательной, так и практической деятельности человека,
направление дальнейшего
развития человеческой цивилизации будет тем или иным. Таким образом, все дело –
в выборе концепции, на основе которой сначала формируется картина
окружающего мира, а затем складывается направление развития цивилизации.
Естественный на первый взгляд вопрос, откуда сознание берет тот набор
концепций, из которых производит упомянутый выбор, может быть, и интересен. Во
всяком случае, он принципиален: что первично, бытие или сознание? Но, пожалуй,
этот вопрос неконструктивен. Откуда взялась энергия, выделившаяся в результате
Большого взрыва (одна из популярных концепций), чем обусловлено возникновение и
структура молекул-репликаторов (другая популярная концепция), мы тоже не знаем.
Но это не повод остановиться в этой точке рассуждений и не сделать попытки
построения дальнейшей теории.
Если все дело в выборе
концепции, то не следует ли подумать о том, какова может быть осознаваемая или
неосознаваемая цель подобного выбора?
ПСИХОЛОГИЧЕСКОЕ ОТСТУПЛЕНИЕ
Рассмотрим психологический
аспект ситуации традиционного познания, понимая под этим не столько
индивидуальное поведение, основанное на какой-либо осознаваемой или
неосознаваемой идее или импульсе, сколько род социального поведения и его
отражение в общении. Предположим, двое играют в следующую игру: у одного
имеется маленькая фишка, которую он прячет в левую или правую руку. Второй должен
угадывать, где фишка. Когда он угадывает, он выигрывает одно очко, когда не
угадывает – проигрывает то же очко. Он делает первую попытку и указывает ту или
иную руку. Первый игрок демонстрирует, где фишка. Это радикально меняет
ситуацию, и перед второй попыткой номер два начинает вычислять. Чтобы выиграть,
он должен угадать, где будет фишка в следующий раз, но ТЕПЕРЬ оба игрока ЗНАЮТ,
где она только что была. Номер два должен оценить способности своего
противника. В различных ситуациях он может рассуждать следующим образом. Если
номер один – ребенок, т.е. человек, который еще не может думать за другого, то,
скорее всего, он просто переложит фишку в другую руку. Если номер первый чуть
более способен к оценке игровой ситуации, он может подумать, что номер второй
сочтет его за ребенка, и чтобы наказать его за ошибку, оставит фишку в той же
руке. Если номер второй решит, что номер первый будет доказывать ему, что он не
ребенок, он догадается, что фишка осталась, где была. Если номер первый в свою
очередь просчитает все это, он переложит фишку, и так далее... Они начнут
"вычислять" друг друга и действовать соответственно. Каждая новая
попытка приносит новую информацию, последовательность результатов можно
подвергнуть анализу, и окончательный результат (после многих попыток) будет не
равновероятен для обоих, но покажет, "кто лучше знает". Причем это
знание будет основано как на анализе последовательности результатов, так и на
точности модели, выбранной для оценки партнера. Этого не могло бы случиться,
если бы номер один был идеальным "генератором случайных чисел"
(поскольку ясно, что именно такая стратегия гарантирует нулевой результат по
окончании игры). Но у обоих из них было априорное намерение выиграть, и это
было главным условием последовавшей "обработки информации".
Хотелось бы подчеркнуть два
обстоятельства. Во-первых, эта игра напоминает некоторый вариант модификации
теста Роршаха, описанной во Введении. Действительно, в каждой новой попытке уже
содержится "идея", встречавшаяся ранее. И, между прочим, почти все
общение людей между собой основано на тех или иных предположениях о мотивах и
поступках другого. Почти каждый конфликт в жизни или в литературном
произведении основан на ошибке, допущенной в оценке другого. Таким образом,
наши ошибки связаны с нашим же моделированием, которое мы делаем заранее. Наши
действия редко спонтанны, и даже когда они кажутся таковыми, трудно не заподозрить, что в этом
случае моделирование было выполнено просто на более глубоком уровне сознания.
Похоже, что у нас всегда есть какая-то цель, осознаем мы это или нет, а если
так, то начинается игра. В какую игру мы играем, занимаясь физикой и окружающим
миром, понять труднее, но выглядит это точно так же. Никому "не
дозволено" начинать изучение природы с самого начала, "изобретение
велосипеда" осуждается, если не запрещается обществом (научным
сообществом). Но, начиная с того места, где уже находятся все остальные, мы
втягиваемся в ту же самую игру.
Во-вторых, имеются
"начальные условия". Мы не можем начать анализировать (строить концепции),
пока не состоится первая попытка. И эта попытка СЛУЧАЙНА. Взаимно дополнительный
характер начальных условий и структуры формального математического описания
отчетливо осознается в теоретической физике и космологии. Но здесь хотелось бы
подчеркнуть случайный характер "начальных условий", первой точки, в
противовес рациональному (и даже материальному) характеру последствий, когда за
дело берется человеческое сознание. Каждое отдельное событие может быть чудом,
но, пытаясь вступить в общение по этому поводу, формируя для этого непротиворечивый
язык, мы создаем Вселенную, которую возможно и наиболее удобно обсуждать.
ИНТЕРПРЕТАЦИЯ НАБЛЮДЕНИЙ
Попытаемся учесть приведенные соображения при
выборе концепции, происходящем наряду с интерпретацией наблюдений.
Представим себе линию, ось,
на которой находится случайно движущаяся частица. В простейшем случае, который
обсуждается чаще всего, эта частица перескакивает на dx метров каждые dt секунд либо в положительном, либо в отрицательном направлении оси, которое
выбирается случайно. Эта модель (случайные блуждания) хорошо известна и имеет
много приложений при статистическом описании процессов. Можно показать, что
среднее смещение частицы относительно начала координат <x> = 0, в то время как среднеквадратичное смещение пропорционально корню
квадратному из числа шагов.
Будем предполагать, что это
блуждание происходит в темноте, и для наблюдения движения частицы используем
стробоскоп, частота вспышек которого значительно меньше, чем частота скачков
частицы. Произведя ряд измерений смещений и времен, мы обнаружим, что
наблюдаемое смещение пропорционально корню квадратному из времени, и
догадаемся, что частица участвует в случайном блуждании с постоянными величиной
и периодом шага. Поскольку мы знаем заранее (но откуда? Ведь это только первый
закон Ньютона о существовании
инерциальных систем отсчета, который является аксиомой хотя и
основной), что свободная частица движется равномерно и прямолинейно
(т.е. ее смещение должно линейно изменяться со временем), и никаких полей мы не
включали, после таких наблюдений придется задуматься о причине этих скачков.
Представим теперь, что
величины и периоды скачков зависят от времени таким образом, что,
наблюдая за движением частицы с помощью стробоскопа, мы видим, что ее смещение
нарастает равномерно. В этом случае мы с удовлетворением заключаем, что частица
движется свободно. Способ нахождения таких зависимостей величин и периодов
скачков от времени описан далее.
Но это означает, что возможно точно так же
найти и другую зависимость параметров скачков от времени, например, такую, что
при наблюдении частицы с помощью стробоскопа мы увидим равноускоренное
движение. И тогда мы займемся поиском источника действующей силы (гравитация?
электростатика?), или сочтем систему отсчета неинерциальной (ускоренной).
Не вздор ли это? Мы видим
то, что видим. Но ведь мы заранее знаем и пребываем в уверенности, что аксиома
об инерциальном движении справедлива, что до сих пор являлось наиболее удобным,
наиболее экономным способом мышления. Даже осознание роли наблюдателя в
квантовой механике не поколебало эту уверенность. Утверждение оказалось в
высшей степени подходящим. Дополнение к модифицированной Роршаховской картинке
очень убедительным.
И, наконец, при чем тут
стробоскоп? При том, что любой эксперимент, который мы можем поставить в
микромире, всегда является в некотором смысле экспериментом со
стробоскопом, непрерывность не достигается.
Конвенциональность характера
любой физической теории ясно осознавалась с начала ХХ века (А.Пуанкаре, 1983).
Сегодня темой обсуждения является необходимость введения в теорию какой-либо
функции сознания наблюдателя в явном виде (Ф.Капра,1994, H.Stapp 1994).
С ТОЧКИ ЗРЕНИЯ ФИЗИКИ
Основной аксиомой (А)
естественных наук является возможность описывать процессы в окружающем мире на
языке логики и математики, принадлежащем человеческому сознанию, причем
возможны два подхода. В первом из них вводится функция Лагранжа и постулируется
принцип наименьшего действия. Будем называть такую возможность аксиомой А(д)
(детерминизм). Результатом применения А(д)-аксиомы являются дифференциальные
уравнения движения -- математические структуры, позволяющие получить
зависимость координат системы от времени, если известны физические поля и
заданы начальные условия. Для проверки этих результатов необходимо выполнить
измерения, т.е. непосредственно определить координаты в различные моменты
времени. После этого расчетные и экспериментальные результаты сопоставляются.
Если имеются расхождения, то говорят о неучтенных полях или процессах
(например, о диссипативных силах и диссипации энергии). Последнее означает, что
от рассмотрения нескольких тел в рамках А(д)-аксиомы следует перейти к учету
дополнительной системы, состоящей из большого числа тел, для которой считается
выполненной аксиома А(с) (статистика): для описания поведения системы,
состоящей из большого числа тел, пригоден формальный аппарат теории
вероятностей и случайных процессов. Упомянутые расхождения между теоретическими
предсказаниями и экспериментальными результатами в механике могут быть
использованы для определения физических констант термодинамического
(статистического) процесса. Используя этот подход, мы также получаем
математические структуры (и некоторые из них имеют смысл дифференциальных
уравнений движения), с помощью которых можно предсказать поведение системы.
Важно отметить, что если мы
попытаемся рассчитать движение микроскопических молекул (образующих систему
многих тел), то мы сталкиваемся с невозможностью прямых измерений координат и
времен и фактически сопоставляем результаты использования А(д) и А(с)
аксиом, что в свою очередь требует непротиворечивости описания.
Имеется еще одно важное
обстоятельство. По мере убывания размеров тел системы мы начинаем оказывать
необратимые воздействия на результаты прямых измерений, причем не только своими
приборами, но и, как подчеркнуто в ( J. A.Wheeler, 1988), самим способом постановки вопросов. Эта ситуация обсуждается в
квантовой теории. Последняя вновь существенно использует статистические идеи, и
детерминированное движение более ни описывается, ни наблюдается. Микроуровень,
на котором детерминистские следствия А(д)-аксиомы классической механики теряют
силу, определяется соотношением неопределенности Гейзенберга. Постоянная Планка
h является количественной характеристикой сферы применимости классической
механики.
Итак, существует переходная
область, в которой следствия А(д)-аксиомы перестают работать с уменьшением
размера объекта и в которой следствия А(с)-аксиомы становятся бессмысленными с
увеличением размера объектов и уменьшением их числа. Что же до прямых
измерений, – то они невозможны по указанным выше причинам.
В то время как
конвенциональный характер микроявлений осознается большинством ученых,
конвенциональныый характер А(д)-аксиомы и ее следствий ясен значительно реже (S.Siparov 1994,1). Это обусловлено
традицией в интерпретации экспериментальных данных в прямом измерении.
Разрабатывая теорию, мы говорим об однородности пространства-времени или о его
кривизне. Но таким же образом мы можем говорить и о случайностных свойствах
физического мира, т.е. стохастические свойства могут проявляться не только на
микроскопическом (G.Catania 1990), но и на макроскопическом уровне и могут наблюдаться в прямых
экспериментах, результаты которых интерпретируются соответствующим образом.
Влияние сознания наблюдателя, которое с очевидностью следует учитывать в
микромире (Ф.Капра, 1994), следует также учитывать и в физике макромира.
ПОСТРОЕНИЕ ФУНКЦИИ СОЗНАНИЯ НАБЛЮДАТЕЛЯ
Перейдем к построению этой
функции сознания наблюдателя и используем упоминавшуюся выше модель случайных
блужданий для развития идей, изложенных в (S.Siparov,
1994,1). Среднее квадратичное смещение в простейшем случае постоянной
величины скачка dx и постоянного промежутка времени между скачками dt равно
(1)
где b --
безразмерная константа. Если потребовать, чтобы отношение dx/dt не являлось ни нулем, ни бесконечностью, то можно получить (У.Феллер,1966)
так называемое уравнение Фоккера-Планка, которое при наличии граничных и
начальных условий позволяет определить вероятность того, что случайно
блуждающая частица будет обнаружена в некоторой окрестности точки x в
момент времени t. Эта модель очень удобна для описания диффузии (в рамках А(с)-подхода),
уравнение которой в точности совпадает по внешнему виду с уравнением
Фоккера-Планка, но результат его решения трактуется как зависимость
концентрации диффундирующего вещества от координаты и времени. Мгновенное распределение
вещества по всему образцу обычно игнорируется (не обсуждается) из соображений
"физического смысла", т.е. тех самых соображений, которые были
использованы при выборе конечного значения 
. Это несложный пример того, что
происходит, когда мы используем формальную математическую модель, порожденную
нашим сознанием, принимаем во внимание только ту ее часть, которая нас
устраивает и называем ее законом природы, если удается пронаблюдать
соответствие между предсказанными результатами и экспериментальными.
Сохраним форму выражения (1)
для зависящих от времени dx и dt и рассмотрим его как решение динамического уравнения, в котором 
играет роль перемещения (особенности такого
предположения будут рассмотрены ниже). Переходя от dx и dt к X(t ) и T(t ) и сохраняя вид уравнения (1), получим
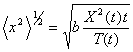(2)
Записывая уравнение (2) в такой форме, мы воспользовались эргодической
гипотезой, согласно которой среднее по реализациям (левая часть уравнения)
совпадает со средним при t à ∞ (правая часть уравнения). Найдем
такие функции X(t) и T(t), что перемещение линейно зависит от времени. Именно в этом случае, наблюдая
движение частицы с помощью стробоскопа, мы обнаружим, что она движется
равномерно. Потребуем, чтобы производная от перемещения была константой. Это
означает, что мы рассматриваем только те (случайные) точки на оси, посещенные частицей,
которые лежат в окрестности заданной прямой x1(t) = vt, v = const.
Вычисляя производную, получим
(3)
Пусть функция T(t) произвольна. Если набор точек,
посещенных частицей, достаточно плотен, то в течение одной вспышки стробоскопа,
длящейся t секунд (причем t >> T(t)), будут наблюдаться точки, для которых длина скачка X(t) удовлетворяет условию (3). Это даст возможность пронаблюдать
равномерное прямолинейное движение частицы, в то время как разброс точек на
графике (связанный со случайным характером процесса) можно интерпретировать как
экспериментальную ошибку.
Таким же образом можно найти
условия, соответствующие другим видам движений -- равноускоренному и т.д. Выбор
линейной функции x1(t) и условия Cs = 0 в
виде уравнения (3) обусловлен их соответствием постулату о существовании
инерциальных систем отсчета. Тем не менее ясно, что в том же самом наборе
посещенных точек мы можем пронаблюдать и другие движения, если
используем другие функции x1(t). Таким образом, функция Cs (где C соответствует Consciousness, а s -- stochastic) есть функция сознания наблюдателя. Необходимость введения такой функции
обсуждалась в (Ф.Капра, 1994, H.Stapp,
1994, G.Catania,
1990). Точно так же и необходимость единого подхода к описанию микро- и
макроявлений осознана давно (Р.Фейнман, А.Хибс, 1968), но до сих пор эта
проблема не решена.
Для того, чтобы произвол в
выборе T(t)
не оказывал влияния при экспериментальном исследовании макроскопических
объектов классической механики, достаточно потребовать, чтобы для больших
значений t величина T(t) была значительно меньше, чем t, что
обычно выполняется для любых измерений.
СЛЕДСТВИЯ
Возвращаясь к концепции
мира, обладающего присущими случайностными свойствами – в том же смысле,
который мы используем, говоря об однородности пространства-времени как о
постулате – можно заметить, что основным законом этой мерцающей Вселенной
является та самая изменчивость, о которой Дж.Уилер писал в (Дж.Уилер, 1982).
Обсуждаемый подход является
непротиворечивым, хотя, конечно, и не предлагает немедленное исчерпывающее
описание всех разделов физической науки. Обсудим его место в существующих
теориях.
1. При построении механики
можно сохранить формализм Лагранжа с тем отличием, что в принципе наименьшего
действия следует перейти от вариационной задачи с закрепленными концами к
вариационной задаче со свободными концами, причем роль условия
трансверсальности будет играть условие Cs = 0. С формальной
стороны это и будет означать следующее: если раньше мы полагали, что
детерминированный мир существует, мы в состоянии его пронаблюдать, зафиксировав
соответствующие координаты и моменты времени, а затем, подобрав аппроксимирующую
функцию, которую и объявляли законом, то теперь мы отдаем себе отчет в том,
что, указывая (произвольный) закон, мы в состоянии пронаблюдать его выполнение
в окружающем мире. Тогда получим:
(4)
Если никаких полей,
связанных со своими источниками, не существует, частица движется свободно (в
мерцающем пространстве-времени), и мы хотим, чтобы в этом случае она двигалась
равномерно и прямолинейно, то следует использовать выражение для Cs,
определяемое формулой (3) и решить систему (4) для нахождения свободного
лагранжиана L0. Усложняя, как обычно, исходную систему,
получим и уравнения движения при наличии полей или сил. В рамках
рассматриваемого подхода можно говорить об однородности и изотропности
пространства-времени только с учетом определенной процедуры осреднения по
некоторой области.
2. Можно также рассмотреть
систему отсчета, в которой свободная частица движется согласно уравнению (1),
т.е. обладает ускорением, убывающим со временем как 
. Такая система станет инерциальной при
больших значениях t (в соответствующих единицах). Это
является аналогией ситуации в общей теории относительности, когда область
пространства-времени вдали от материальных масс обладает исчезающе малой
кривизной.
3. При построении
электродинамики в обсуждаемом случайно мерцающем пространстве-времени можно
воспользоваться соответствующими результатами для дискретного пространства,
например (К.Е.Плохотников, 1988).
4. В квантовой механике
перенос привычных случайностных свойств микроскопического объекта на
пространство-время (G.Catania, 1990) позволит описать
взаимодействие квантовой частицы с прибором с единых позиций. Кроме того,
конечность первого интервала 
соответствует идеям и результатам, изложенным в работе (D.Kobe, V.Aquilera-Navarro 1994), посвященной выводу соотношения неопределенности для энергии и
времени.
5. В специальной теории
относительности появление второго постулата о предельном значении скорости
связано с теорией электромагнетизма Максвелла. Но если частица движется согласно
уравнению (2), то имеется предельное значение скорости, присущее
непосредственно данному подходу. Действительно, например, для простейшего
случая ур.(1) зависимость x(t) представляет собой распределение точек около ветви параболы. Вычисляя
дисперсии D(t) и D(t+dt), полагая dt >> dτ, получим предельное значение скорости v = (1/2)dD(t)/dt. Это означает, что, хотя
"сверхсветовая" скорость и возможна, наблюдать ее можно только в
случае, если время одного измерения t меньше чем dt (или
t < T(t) в более сложном случае). Такое движение
в окрестности параболы связано с выбором в
качестве смещения.
6. У параболы имеется две
ветви, и случайно блуждающая частица может быть обнаружена по очереди возле
каждой из них (прямой аналогией является смена лидера у игроков в «орлянку»).
Как показано в (У.Феллер, 1967), такие переходы (такая смена) происходят
гораздо реже, чем это может показаться, более того, их частота убывает, как 
. Можно интерпретировать такие переходы,
например, как аналогию к переходам от стадии расширения к стадии сжатия
Вселенной в терминах Фридмановского подхода к общей теории относительности.
7. Как было показано
Е.Реками (E.Recami 1979) в рамках обобщенной теории относительности, первое, что увидит
наблюдатель при наблюдении сверхсветовых космологических объектов, будет
вспышка в некоторой точке, затем светящаяся точка раздвоится, и на первом этапе
наблюдений скорость расхождения светящихся точек будет пропорциональна .
Это соответствует предположению о том, что при малых временах (в
соответствующих единицах), когда T(t) не достаточно мало, чтобы удовлетворить
условию t
> T(t),
движение описывается формулой (2), из которой также следует, что
скорость пропорциональна 
.
Следует
отметить, что два независимых фундаментальных постулата (существование
инерциальных систем отсчета и существование предельной скорости) заменяются
одним – существование у мира случайностных свойств, – из которого оба указанных
являются следствием. В традиционной теории результатом наблюдения является
состояние квантового объекта. При данном подходе наблюдатель участвует в
создании всего мира. Уравнения физических законов представляют собой лишь
некоторые структуры, налагаемые на мир и порождаемые сознанием наблюдателя. Из
всего набора случайных точек-событий наблюдаются те, что наилучшим образом
удовлетворяют избранной структуре. Это означает, что сознание, сформировавшее произвольную
картину мира, наделившее его некоторыми свойствами и построившее
непротиворечивую структуру для его описания, осуществит и его наблюдение,
наблюдая тем самым само себя. Результаты такого наблюдения, предъявленные
другому сознанию, помогут сформировать в этом другом сознании ту же картину с
теми же свойствами, что, в конце концов, приведет к материализации мира: за
огромным количеством дополнительных точек и линий, нанесенных всевозможными
наблюдателями, становится незаметным случайный характер исходного объекта, все
видят (и наблюдают в экспериментах любого вида) то, договоренность о чем
складывалась на протяжении всей человеческой истории.
ЗАКЛЮЧЕНИЕ
Осознание существования беспричинных событий
позволяет подойти к конструированию желаемого космоса (т.е. мира, обладающего
заданными свойствами). С этой целью
необходимо, во-первых, сформулировать систему аксиом, являющихся
"первым наблюдением" в том же смысле, что и при рассмотрении пятна Роршаха, а во-вторых, так преобразовать
формальный аппарат (например, подход Гамильтона-Лагранжа при построении основ
физической теории), чтобы получить возможность описывать заранее заданные
свойства. Тогда вопросы, задаваемые природе
путем постановки экспериментов, будут отличаться от задаваемых в
настоящее время, а ответы будут
удовлетворять или неудовлетворять нас на ином, отличном пути познания, ведущем
к построению иной реальности. Таким образом, так называемый реальный окружающий
мир оказывается не единственным, а одним из равноправно возможных и объективно
осуществимых. Признание одновременного существования всех мыслимых вселенных (H.
ЛИТЕРАТУРА К ГЛАВЕ
G.Catania.
"The need for a probabilistic interpretation of Quantum
Mechanics: causes and results". Proc.Conf.on
Found.of Math.and Phys.,
H.
Everett. Rev.Mod.Phys., 29, 454, 1957 .
П.Дэвис. Случайная вселенная. М.Мир, 1985.
У.Феллер. Введение в теорию вероятностей и ее приложения. М.,
"Мир", 1967.
Р.Фейнман, А.Хибс. Квантовая механика и интегралы по траекториям.
М.,"Мир", 1968.
Ф.Капра. Дао физики. Спб., "Орис", 1994.
D.H.Kobe,
V.C.Aquilera-Navarro. "Derivation
of the energy-time
uncertainty relation". Phys.Rev.A, v.50, No.2, p.933-938, 1994.
К.Е.Плохотников. ДАН т.301, с.1362, 1988.
А.Пуанкаре. О науке. М."Наука", 1983.
E.Recami. "Relativity Theory and its Generalization", Astrofisica e Cosmologia Gravitazione Quanti e Relativita, (Guinti Barbera, Firenze, 1979).
S.Siparov. "Conventional Character
of Physical Theories".
Proc.Conf."Physical
Interpretations of Relativity Theory", Suppl. Papers,
p.80-86,
S.Siparov. "Inversion in
the cognition process
and reorganization of personality".
Report
to the 5-th Conf. of the ESSSAT,
Slawianowski J.J. Platonism as a Spontaneous Way of
Thinking in Modern Physics. Report to the 6-th Conference of the
ESSSAT,
H.P.Stapp. "Theoretical model
of a purported
empirical violation of the
predictions of quantum
theory". Phys.Rev.A, vol.50,
No.1, p.18, 1994.
Дж.А.Уилер. Квант и Вселенная. В сб. Астрофизика, кванты и теория
относительности. М., "Мир", 1982.
J.A.Wheeler.
World as system self-synthesized by
quantum networking. IBM J. Res. Develop. vol.32, No.1, 1988.
*Эта
дополнительная глава опубликована в виде статей в
1) С.Сипаров. Физический мир как функция сознаниа
наблюдателя или реальность как мифологема хаоса. «Размышления о хаосе»,
С-Петербург, с.37, 1997
2) S.Siparov. The Physical World as a Function of the Observer's
Consciousness. In: Studies in Science & Theology, v.5, Labor et Fides,
